Application: Linear Advection Equation
The 5th order CRWENO scheme is applied to the linear advection equation. A smooth solution is considered on a periodic domain to analyze the accuracy and convergence properties of the new scheme.
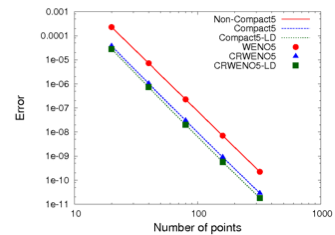
The CRWENO schemes show a significantly lower absolute error than the WENO scheme, for the same order of convergence.
While the CRWENO scheme is computationally more expensive than the WENO scheme (since it requires a tridiagonal inversion at each time step), it is more computationally efficient, i.e., for solutions with the same error, the CRWENO scheme is faster (since it requires a coarser grid).
The CRWENO scheme is applied to a solution containing different waveforms - exponential, square, triangular, parabolic. It shows improved resolution, compared to the WENO scheme. The exponential wave shows significantly lower clipping while the square wave suffers for reduced smearing.
Contact: ghosh (at) mcs (dot) anl (dot) gov

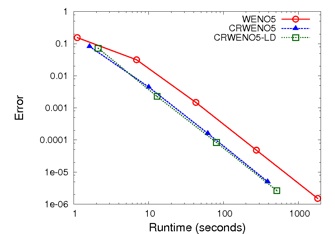
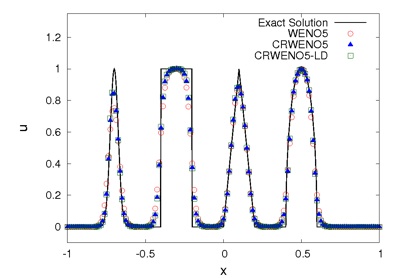
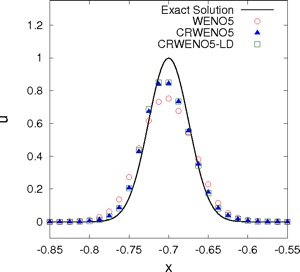
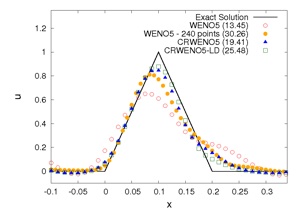
The CRWENO schemes are more computationally efficient for discontinuous problems. The number in the parentheses for the numerical solutions to a triangular wave are the computational run-times. The CRWENO5 schemes yield solutions on a 160-point grid that are comparable to the WENO5 solution on a 240-point grid, while being less expensive.
